Arithmetic and_logic_operation/Instruction set architecture

ریاضی اور_لاگ_اپریشن / انسٹرکشن سیٹ فن تعمیر: کمپیوٹر سائنس میں ، انسٹرکشن سیٹ آرکیٹیکچر ( ISA ) ، جسے کمپیوٹر فن تعمیر بھی کہا جاتا ہے ، ایک کمپیوٹر کا خلاصہ ماڈل ہے۔ ایک ایسا آلہ جو اس ISA کے ذریعہ بیان کردہ ہدایات پر عملدرآمد کرتا ہے ، جیسے سینٹرل پروسیسنگ یونٹ (سی پی یو) ، کو عمل درآمد کہا جاتا ہے۔
ریاضی اور_لاگ_اسٹرکچر / ریاضی کی منطق اکائی: کمپیوٹنگ میں ، ایک ریاضی کا منطق یونٹ (ALU) ایک مشترکہ ڈیجیٹل سرکٹ ہے جو عددی بائنری نمبروں پر ریاضی اور بٹویس آپریشن انجام دیتا ہے۔ یہ فلوٹنگ پوائنٹ یونٹ (FPU) کے برعکس ہے ، جو فلوٹنگ پوائنٹ نمبرز پر کام کرتا ہے۔ یہ کمپیوٹنگ سرکٹوں کی بہت سی اقسام کا بنیادی عمارت ہے ، جس میں کمپیوٹروں کی سنٹرل پروسیسنگ یونٹ (سی پی یو) ، ایف پی یو ، اور گرافکس پروسیسنگ یونٹ (جی پی یو) شامل ہیں۔
ریاضی اور_ بلاگ_ یونیت / ریاضی کی منطق یونٹ: کمپیوٹنگ میں ، ایک ریاضی کا منطق یونٹ (ALU) ایک مشترکہ ڈیجیٹل سرکٹ ہے جو عددی بائنری نمبروں پر ریاضی اور بٹویس آپریشن انجام دیتا ہے۔ یہ فلوٹنگ پوائنٹ یونٹ (FPU) کے برعکس ہے ، جو فلوٹنگ پوائنٹ نمبرز پر کام کرتا ہے۔ یہ کمپیوٹنگ سرکٹوں کی بہت سی اقسام کا بنیادی عمارت ہے ، جس میں کمپیوٹروں کی سنٹرل پروسیسنگ یونٹ (سی پی یو) ، ایف پی یو ، اور گرافکس پروسیسنگ یونٹ (جی پی یو) شامل ہیں۔
ریاضی اور_ لاجیکل_ یونیت / ریاضی کی منطق اکائی: کمپیوٹنگ میں ، ایک ریاضی کا منطق یونٹ (ALU) ایک مشترکہ ڈیجیٹل سرکٹ ہے جو عددی بائنری نمبروں پر ریاضی اور بٹویس آپریشن انجام دیتا ہے۔ یہ فلوٹنگ پوائنٹ یونٹ (FPU) کے برعکس ہے ، جو فلوٹنگ پوائنٹ نمبرز پر کام کرتا ہے۔ یہ کمپیوٹنگ سرکٹوں کی بہت سی اقسام کا بنیادی عمارت ہے ، جس میں کمپیوٹروں کی سنٹرل پروسیسنگ یونٹ (سی پی یو) ، ایف پی یو ، اور گرافکس پروسیسنگ یونٹ (جی پی یو) شامل ہیں۔
حسابی اوسط / اوسط: بول چال کی زبان میں ، اوسطا واحد نمبر ہے جو نمبروں کی خالی فہرست کے نمائندے کے طور پر لیا جاتا ہے۔ اوسط کے مختلف تصورات مختلف سیاق و سباق میں مستعمل ہیں۔ اکثر "اوسط" سے ریاضی کے معنی مراد ہوتے ہیں ، اعداد کا مجموعہ جس میں تقسیم کیا جاتا ہے کہ اوسطا کتنی تعداد کی جارہی ہے۔ اعدادوشمار میں ، وسط ، اوسط اور موڈ سب کو مرکزی رجحان کے اقدامات کے طور پر جانا جاتا ہے ، اور بول چال کے استعمال میں ان میں سے کسی کو بھی اوسط قدر کہا جاسکتا ہے۔
ریاضی بلئرڈس / ریاضی بلئرڈس: تفریحی ریاضی میں ، ریاضی بلئرڈز ایک ہندسی طریقہ فراہم کرتے ہیں جس میں ایک مستطیل کے اندر عکاسی کا استعمال کرتے ہوئے کم سے کم عام متعدد اور دو قدرتی اعداد کا سب سے بڑا عام تفریق معلوم کیا جاتا ہے جس کے اطراف دو دیئے گئے اعداد ہیں۔ یہ متحرک بلئرڈز کے چکر کے تجزیہ کی ایک آسان مثال ہے۔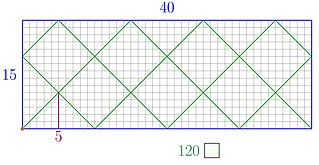
ریاضی سرکٹ / ریاضی سرکٹ پیچیدگی: کمپیوٹیشنل پیچیدگی کے نظریہ میں ، ریاضی کے سرکٹس کثیر القومی کمپیوٹنگ کے لئے معیاری ماڈل ہیں۔ غیر رسمی طور پر ، ایک ریاضی کا سرکٹ ان پٹ کو یا تو متغیرات یا اعداد کے طور پر لیتا ہے ، اور اسے پہلے سے ہی گنتی والے دو تاثرات کو شامل کرنے یا ضرب کرنے کی اجازت ہے۔ ریاضی کے سرکٹس کمپیوٹنگ کثیر الاضلاع کی پیچیدگی کو سمجھنے کا باقاعدہ طریقہ فراہم کرتے ہیں۔ تحقیق کی اس سطر میں بنیادی نوعیت کا سوال یہ ہے کہ "دیئے گئے کثیرالعد کی گنتی کا سب سے موثر طریقہ کیا ہے؟ "
ریاضی سرکٹ_سوٹ / ریاضی کے سرکٹ کی پیچیدگی: کمپیوٹیشنل پیچیدگی کے نظریہ میں ، ریاضی کے سرکٹس کثیر القومی کمپیوٹنگ کے لئے معیاری ماڈل ہیں۔ غیر رسمی طور پر ، ایک ریاضی کا سرکٹ ان پٹ کو یا تو متغیرات یا اعداد کے طور پر لیتا ہے ، اور اسے پہلے سے ہی گنتی والے دو تاثرات کو شامل کرنے یا ضرب کرنے کی اجازت ہے۔ ریاضی کے سرکٹس کمپیوٹنگ کثیر الاضلاع کی پیچیدگی کو سمجھنے کا باقاعدہ طریقہ فراہم کرتے ہیں۔ تحقیق کی اس سطر میں بنیادی نوعیت کا سوال یہ ہے کہ "دیئے گئے کثیرالعد کی گنتی کا سب سے موثر طریقہ کیا ہے؟ "
ریاضی سرکٹ_کمپلٹی / ریاضی کے سرکٹ کی پیچیدگی: کمپیوٹیشنل پیچیدگی کے نظریہ میں ، ریاضی کے سرکٹس کثیر القومی کمپیوٹنگ کے لئے معیاری ماڈل ہیں۔ غیر رسمی طور پر ، ایک ریاضی کا سرکٹ ان پٹ کو یا تو متغیرات یا اعداد کے طور پر لیتا ہے ، اور اسے پہلے سے ہی گنتی والے دو تاثرات کو شامل کرنے یا ضرب کرنے کی اجازت ہے۔ ریاضی کے سرکٹس کمپیوٹنگ کثیر الاضلاع کی پیچیدگی کو سمجھنے کا باقاعدہ طریقہ فراہم کرتے ہیں۔ تحقیق کی اس سطر میں بنیادی نوعیت کا سوال یہ ہے کہ "دیئے گئے کثیرالعد کی گنتی کا سب سے موثر طریقہ کیا ہے؟ "
ریاضی کے سرکٹس_کمپلٹی / ریاضی سرکٹ کی پیچیدگی: کمپیوٹیشنل پیچیدگی کے نظریہ میں ، ریاضی کے سرکٹس کثیر القومی کمپیوٹنگ کے لئے معیاری ماڈل ہیں۔ غیر رسمی طور پر ، ایک ریاضی کا سرکٹ ان پٹ کو یا تو متغیرات یا اعداد کے طور پر لیتا ہے ، اور اسے پہلے سے ہی گنتی والے دو تاثرات کو شامل کرنے یا ضرب کرنے کی اجازت ہے۔ ریاضی کے سرکٹس کمپیوٹنگ کثیر الاضلاع کی پیچیدگی کو سمجھنے کا باقاعدہ طریقہ فراہم کرتے ہیں۔ تحقیق کی اس سطر میں بنیادی نوعیت کا سوال یہ ہے کہ "دیئے گئے کثیرالعد کی گنتی کا سب سے موثر طریقہ کیا ہے؟ "
حسابی کوڈ / ریاضی کوڈنگ: ریاضی کوڈنگ ( AC ) اینٹراپی انکوڈنگ کی ایک شکل ہے جو بے عیب ڈیٹا کمپریشن میں استعمال ہوتی ہے۔ عام طور پر ، حرف کی ایک تار جیسے "ہیلو وہاں" جیسے الفاظ ASCII کوڈ کی طرح ، فی حرف بٹس کی ایک مقررہ تعداد کا استعمال کرتے ہوئے کی نمائندگی کرتے ہیں۔ جب تار کو حسابی انکوڈنگ میں تبدیل کیا جاتا ہے تو ، کثرت سے استعمال ہونے والے حروف کم بٹس کے ساتھ ذخیرہ ہوجائیں گے اور نہ ہی اکثر ہونے والے حروف زیادہ بٹس کے ساتھ ذخیرہ ہوجائیں گے ، جس کے نتیجے میں مجموعی طور پر کم بٹس استعمال ہوں گے۔ ریاضی کے کوڈنگ انٹروپی انکوڈنگ کی دوسری شکلوں سے مختلف ہے ، جیسے ہف مین کوڈنگ ، ان پٹ کو جزو کی علامتوں میں الگ کرنے اور ہر ایک کو کوڈ کے ساتھ بدلنے کے بجائے ، ریاضی کے کوڈنگ نے پورے پیغام کو ایک ہی نمبر میں ، ایک صوابدیدی صحت سے متعلق فریکشن کیو ، جہاں 0.0 ≤ Q <1.0 . یہ موجودہ اعداد و شمار کو ایک حد کے طور پر ظاہر کرتا ہے ، جس کی وضاحت دو نمبروں سے ہوتی ہے۔ اینٹروپی کوڈرز کا ایک حالیہ خاندان جس کو غیر متمم اعدادی نظام کہا جاتا ہے ، موجودہ معلومات کی نمائندگی کرنے والی واحد قدرتی تعداد پر براہ راست کام کرنے کے بدولت تیز رفتار عمل درآمد کی اجازت دیتا ہے۔
حسابی کوڈر / ریاضی کوڈنگ: ریاضی کوڈنگ ( AC ) اینٹراپی انکوڈنگ کی ایک شکل ہے جو بے عیب ڈیٹا کمپریشن میں استعمال ہوتی ہے۔ عام طور پر ، حرف کی ایک تار جیسے "ہیلو وہاں" جیسے الفاظ ASCII کوڈ کی طرح ، فی حرف بٹس کی ایک مقررہ تعداد کا استعمال کرتے ہوئے کی نمائندگی کرتے ہیں۔ جب تار کو حسابی انکوڈنگ میں تبدیل کیا جاتا ہے تو ، کثرت سے استعمال ہونے والے حروف کم بٹس کے ساتھ ذخیرہ ہوجائیں گے اور نہ ہی اکثر ہونے والے حروف زیادہ بٹس کے ساتھ ذخیرہ ہوجائیں گے ، جس کے نتیجے میں مجموعی طور پر کم بٹس استعمال ہوں گے۔ ریاضی کے کوڈنگ انٹروپی انکوڈنگ کی دوسری شکلوں سے مختلف ہے ، جیسے ہف مین کوڈنگ ، ان پٹ کو جزو کی علامتوں میں الگ کرنے اور ہر ایک کو کوڈ کے ساتھ بدلنے کے بجائے ، ریاضی کے کوڈنگ نے پورے پیغام کو ایک ہی نمبر میں ، ایک صوابدیدی صحت سے متعلق فریکشن کیو ، جہاں 0.0 ≤ Q <1.0 . یہ موجودہ اعداد و شمار کو ایک حد کے طور پر ظاہر کرتا ہے ، جس کی وضاحت دو نمبروں سے ہوتی ہے۔ اینٹروپی کوڈرز کا ایک حالیہ خاندان جس کو غیر متمم اعدادی نظام کہا جاتا ہے ، موجودہ معلومات کی نمائندگی کرنے والی واحد قدرتی تعداد پر براہ راست کام کرنے کے بدولت تیز رفتار عمل درآمد کی اجازت دیتا ہے۔
حسابی کوڈنگ / ریاضی کوڈنگ: ریاضی کوڈنگ ( AC ) اینٹراپی انکوڈنگ کی ایک شکل ہے جو بے عیب ڈیٹا کمپریشن میں استعمال ہوتی ہے۔ عام طور پر ، حرف کی ایک تار جیسے "ہیلو وہاں" جیسے الفاظ ASCII کوڈ کی طرح ، فی حرف بٹس کی ایک مقررہ تعداد کا استعمال کرتے ہوئے کی نمائندگی کرتے ہیں۔ جب تار کو حسابی انکوڈنگ میں تبدیل کیا جاتا ہے تو ، کثرت سے استعمال ہونے والے حروف کم بٹس کے ساتھ ذخیرہ ہوجائیں گے اور نہ ہی اکثر ہونے والے حروف زیادہ بٹس کے ساتھ ذخیرہ ہوجائیں گے ، جس کے نتیجے میں مجموعی طور پر کم بٹس استعمال ہوں گے۔ ریاضی کے کوڈنگ انٹروپی انکوڈنگ کی دوسری شکلوں سے مختلف ہے ، جیسے ہف مین کوڈنگ ، ان پٹ کو جزو کی علامتوں میں الگ کرنے اور ہر ایک کو کوڈ کے ساتھ بدلنے کے بجائے ، ریاضی کے کوڈنگ نے پورے پیغام کو ایک ہی نمبر میں ، ایک صوابدیدی صحت سے متعلق فریکشن کیو ، جہاں 0.0 ≤ Q <1.0 . یہ موجودہ اعداد و شمار کو ایک حد کے طور پر ظاہر کرتا ہے ، جس کی وضاحت دو نمبروں سے ہوتی ہے۔ اینٹروپی کوڈرز کا ایک حالیہ خاندان جس کو غیر متمم اعدادی نظام کہا جاتا ہے ، موجودہ معلومات کی نمائندگی کرنے والی واحد قدرتی تعداد پر براہ راست کام کرنے کے بدولت تیز رفتار عمل درآمد کی اجازت دیتا ہے۔
ریاضی کے امتزاج / ریاضی کے امتزاج: ریاضی میں ، ریاضی کے کمبینیٹرکس نمبر تھیوری ، کمبینیٹرکس ، ایرگوڈک تھیوری اور ہارمونک تجزیے کے چوراہے کا ایک ایسا میدان ہے۔
ریاضی کی پیچیدگی_کی_اس_ڈسکریٹ_فوریئر_ٹرانسفارم / فاسٹ فوریئر ٹرانسفارم: ایک فاسٹ فوریئر ٹرانسفارم ( FFT ) ایک الگورتھم ہے جو کسی تسلسل کے مجرد فوریئر ٹرانسفارم (DFT) ، یا اس کے الٹا (IDFT) کی گنتی کرتا ہے۔ فوئیر تجزیہ اپنے اصل ڈومین سے اشارے کو فریکوینسی ڈومین میں نمائندگی اور اس کے برعکس تبدیل کرتا ہے۔ DFT مختلف تعدد کے اجزاء میں اقدار کے تسلسل کو گل کر کے حاصل کیا جاتا ہے۔ یہ عمل بہت سے شعبوں میں کارآمد ہے ، لیکن اس کی تعریف سے براہ راست کمپیوٹنگ کرنا عملی طور پر بہت ہی آہستہ ہوتا ہے۔ ایک ایف ایف ٹی تیزی سے ڈی ایف ٹی میٹرکس کو ویرل عوامل کی پیداوار میں اس طرح کی تبدیلیوں کا حساب دیتا ہے۔ نتیجے کے طور پر ، یہ DFT کی کمپیوٹنگ کی پیچیدگی کو کم کرنے کا انتظام کرتا ہے ، جو اس وقت پیدا ہوتا ہے اگر کوئی صرف DFT کی تعریف کا اطلاق کرتا ہے ، کہاں ڈیٹا کا سائز ہے۔ رفتار میں فرق بہت زیادہ ہوسکتا ہے ، خاص طور پر لمبے اعداد و شمار کے سیٹ کے لئے جہاں N ہزاروں یا لاکھوں میں ہوسکتا ہے۔ راؤنڈ آف غلطی کی موجودگی میں ، بہت سے FFT الگورتھم براہ راست یا بالواسطہ DFT تعریف کی جانچ کرنے سے کہیں زیادہ درست ہیں۔ بہت سارے مختلف ایف ایف ٹی الگورتھم شائع شدہ نظریات کی وسیع رینج پر مبنی ہیں ، جن میں سادہ پیچیدہ نمبر ریاضی سے لے کر گروپ تھیوری اور نمبر تھیوری تک ہے۔
ریاضی میں پیچیدگی ایک فاسٹ فوریئر ٹرانسفارم ( FFT ) ایک الگورتھم ہے جو کسی تسلسل کے مجرد فوریئر ٹرانسفارم (DFT) ، یا اس کے الٹا (IDFT) کی گنتی کرتا ہے۔ فوئیر تجزیہ اپنے اصل ڈومین سے اشارے کو فریکوینسی ڈومین میں نمائندگی اور اس کے برعکس تبدیل کرتا ہے۔ DFT مختلف تعدد کے اجزاء میں اقدار کے تسلسل کو گل کر کے حاصل کیا جاتا ہے۔ یہ عمل بہت سے شعبوں میں کارآمد ہے ، لیکن اس کی تعریف سے براہ راست کمپیوٹنگ کرنا عملی طور پر بہت ہی آہستہ ہوتا ہے۔ ایک ایف ایف ٹی تیزی سے ڈی ایف ٹی میٹرکس کو ویرل عوامل کی پیداوار میں اس طرح کی تبدیلیوں کا حساب دیتا ہے۔ نتیجے کے طور پر ، یہ DFT کی کمپیوٹنگ کی پیچیدگی کو کم کرنے کا انتظام کرتا ہے ، جو اس وقت پیدا ہوتا ہے اگر کوئی صرف DFT کی تعریف کا اطلاق کرتا ہے ، کہاں ڈیٹا کا سائز ہے۔ رفتار میں فرق بہت زیادہ ہوسکتا ہے ، خاص طور پر لمبے اعداد و شمار کے سیٹ کے لئے جہاں N ہزاروں یا لاکھوں میں ہوسکتا ہے۔ راؤنڈ آف غلطی کی موجودگی میں ، بہت سے FFT الگورتھم براہ راست یا بالواسطہ DFT تعریف کی جانچ کرنے سے کہیں زیادہ درست ہیں۔ بہت سارے مختلف ایف ایف ٹی الگورتھم شائع شدہ نظریات کی وسیع رینج پر مبنی ہیں ، جن میں سادہ پیچیدہ نمبر ریاضی سے لے کر گروپ تھیوری اور نمبر تھیوری تک ہے۔
ریاضی کی اخترتی_تھیری / بین الثالث ٹیچلملر تھیوری: ریاضی کے ماہر شناسی ماچیزوکی نے بین الثانی ٹیچمولر تھیوری کا نام ہے جو انھوں نے ریاضی کے ریاضی میں اپنے پہلے کام کے بعد 2000 کے دہائی میں تیار کیا تھا۔ موچوزوکی کے مطابق ، یہ "بیضوی منحنی خطوط سے لیس نمبر والے شعبوں کے لئے ٹیچلملر تھیوری کا ایک ریاضی ورژن ہے"۔ ان کی ویب سائٹ پر 2012 میں شائع ہونے والے چار پری پرنٹس کی ایک سیریز میں یہ نظریہ عام کیا گیا تھا۔ اس نظریہ کی سب سے حیرت انگیز دعویدار درخواست یہ ہے کہ نمبر تھیوری میں مختلف بقایا قیاسیوں کے لئے ایک ثبوت مہیا کیا جائے ، خاص طور پر عبق قیاقی ۔ موچوزوکی اور کچھ دوسرے ریاضی دانوں کا دعویٰ ہے کہ یہ نظریہ واقعتا such اس طرح کا ثبوت پیش کرتا ہے لیکن اب تک اس کو ریاضی کی جماعت نے قبول نہیں کیا ہے۔
ریاضی کی کثافت / قدرتی کثافت: تعداد کے نظریہ میں ، قدرتی کثافت اس پیمائش کے ل measure ایک طریقہ ہے کہ قدرتی اعداد کے سیٹ کا ایک ذیلی سیٹ "کتنا بڑا" ہے۔ اس وقفہ کے ذریعے تلاشی جب مطلوبہ اپسمچی کے ارکان کا سامنا کے امکانات پر بنیادی طور پر انحصار کرتی ہے [1، N] N بڑے بڑھنے کے ساتھ.
ریاضی کے ماخوذ / ریاضی کے ماخوذ: نمبر تھیوری میں ، لیگاریس ریاضی کے مشتق ، یا اعداد مشتق ، ایک افعال کے لئے متعین ایک فعل ہے جس کی بنیاد عنصر پر مبنی ہے ، مصنوع کے اخذ کرنے کے لئے مصنوع کے قاعدے کے ساتھ مشابہت ہے جس کا استعمال ریاضیاتی تجزیہ میں ہوتا ہے۔
ریاضی کی حرکیات / ریاضی کی حرکیات: ریاضی کی حرکیات ایک ایسا فیلڈ ہے جو ریاضی ، حرکیاتی نظام اور نمبر تھیوری کے دو شعبوں کو یکجا کرتا ہے۔ کلاسیکی طور پر ، مجرد حرکیات سے مراد پیچیدہ ہوائی جہاز یا اصلی لائن کے خود نقشہ جات کی تکرار کا مطالعہ ہوتا ہے۔ ریاضی کی حرکیات متعدد یا عقلی فعل کے بار بار اطلاق کے تحت عددی ، عقلی ، پی- ایڈک ، اور / یا الجبری نقطہ کی تعداد نظریاتی خصوصیات کا مطالعہ ہے۔ ایک بنیادی مقصد بنیادی ہندسی ساختوں کے معاملے میں ریاضی کی خصوصیات کو بیان کرنا ہے۔
حسابی انکوڈر / ریاضی کوڈنگ: ریاضی کوڈنگ ( AC ) اینٹراپی انکوڈنگ کی ایک شکل ہے جو بے عیب ڈیٹا کمپریشن میں استعمال ہوتی ہے۔ عام طور پر ، حرف کی ایک تار جیسے "ہیلو وہاں" جیسے الفاظ ASCII کوڈ کی طرح ، فی حرف بٹس کی ایک مقررہ تعداد کا استعمال کرتے ہوئے کی نمائندگی کرتے ہیں۔ جب تار کو حسابی انکوڈنگ میں تبدیل کیا جاتا ہے تو ، کثرت سے استعمال ہونے والے حروف کم بٹس کے ساتھ ذخیرہ ہوجائیں گے اور نہ ہی اکثر ہونے والے حروف زیادہ بٹس کے ساتھ ذخیرہ ہوجائیں گے ، جس کے نتیجے میں مجموعی طور پر کم بٹس استعمال ہوں گے۔ ریاضی کے کوڈنگ انٹروپی انکوڈنگ کی دوسری شکلوں سے مختلف ہے ، جیسے ہف مین کوڈنگ ، ان پٹ کو جزو کی علامتوں میں الگ کرنے اور ہر ایک کو کوڈ کے ساتھ بدلنے کے بجائے ، ریاضی کے کوڈنگ نے پورے پیغام کو ایک ہی نمبر میں ، ایک صوابدیدی صحت سے متعلق فریکشن کیو ، جہاں 0.0 ≤ Q <1.0 . یہ موجودہ اعداد و شمار کو ایک حد کے طور پر ظاہر کرتا ہے ، جس کی وضاحت دو نمبروں سے ہوتی ہے۔ اینٹروپی کوڈرز کا ایک حالیہ خاندان جس کو غیر متمم اعدادی نظام کہا جاتا ہے ، موجودہ معلومات کی نمائندگی کرنے والی واحد قدرتی تعداد پر براہ راست کام کرنے کے بدولت تیز رفتار عمل درآمد کی اجازت دیتا ہے۔
ریاضی انکوڈنگ / ریاضی کوڈنگ: ریاضی کوڈنگ ( AC ) اینٹراپی انکوڈنگ کی ایک شکل ہے جو بے عیب ڈیٹا کمپریشن میں استعمال ہوتی ہے۔ عام طور پر ، حرف کی ایک تار جیسے "ہیلو وہاں" جیسے الفاظ ASCII کوڈ کی طرح ، فی حرف بٹس کی ایک مقررہ تعداد کا استعمال کرتے ہوئے کی نمائندگی کرتے ہیں۔ جب تار کو حسابی انکوڈنگ میں تبدیل کیا جاتا ہے تو ، کثرت سے استعمال ہونے والے حروف کم بٹس کے ساتھ ذخیرہ ہوجائیں گے اور نہ ہی اکثر ہونے والے حروف زیادہ بٹس کے ساتھ ذخیرہ ہوجائیں گے ، جس کے نتیجے میں مجموعی طور پر کم بٹس استعمال ہوں گے۔ ریاضی کے کوڈنگ انٹروپی انکوڈنگ کی دوسری شکلوں سے مختلف ہے ، جیسے ہف مین کوڈنگ ، ان پٹ کو جزو کی علامتوں میں الگ کرنے اور ہر ایک کو کوڈ کے ساتھ بدلنے کے بجائے ، ریاضی کے کوڈنگ نے پورے پیغام کو ایک ہی نمبر میں ، ایک صوابدیدی صحت سے متعلق فریکشن کیو ، جہاں 0.0 ≤ Q <1.0 . یہ موجودہ اعداد و شمار کو ایک حد کے طور پر ظاہر کرتا ہے ، جس کی وضاحت دو نمبروں سے ہوتی ہے۔ اینٹروپی کوڈرز کا ایک حالیہ خاندان جس کو غیر متمم اعدادی نظام کہا جاتا ہے ، موجودہ معلومات کی نمائندگی کرنے والی واحد قدرتی تعداد پر براہ راست کام کرنے کے بدولت تیز رفتار عمل درآمد کی اجازت دیتا ہے۔
ریاضی کا اظہار / اظہار (ریاضی): ریاضی میں ، اظہار یا ریاضیاتی اظہار علامتوں کا ایک محدود مجموعہ ہوتا ہے جو قواعد کے مطابق اچھی طرح سے تشکیل پایا جاتا ہے جو سیاق و سباق پر منحصر ہوتا ہے۔ ریاضی کی علامتیں نمبر (مستقل) ، متغیر ، عمل ، افعال ، خط وحدت ، رموز ، اور گروہ بندی کو آپریشن کے ترتیب ، اور منطقی نحو کے دیگر پہلوؤں کا تعین کرنے میں مدد فراہم کرسکتی ہیں۔
والدین کیلئے ریاضی / ریاضی کے لئے ریاضی: والدین کے لیے ریاضی ریاضی کی تعلیم میں والدین اور اساتذہ کا مقصد کے بارے میں ایک کتاب ہے.
والدین کے لئے ریاضی / ریاضی / ریاضی کے لئے ریاضی: والدین کے لیے ریاضی ریاضی کی تعلیم میں والدین اور اساتذہ کا مقصد کے بارے میں ایک کتاب ہے.
ریاضی کا فارمولا / پیانو محور: ریاضی کی منطق میں ، پیانو محور ، جسے ڈیڈکِند – پیانو محور یا پیانو پوسٹولیٹ بھی کہا جاتا ہے ، ان قدرتی تعداد کے محور ہیں جو 19 ویں صدی کے اطالوی ریاضی دان جیسیپی پیانو نے پیش کیے تھے۔ یہ محاورے متعدد میٹامیٹیمیکل تحقیقات میں تقریبا un بدلاؤ استعمال کیے گئے ہیں ، جس میں بنیادی نظریات کی تحقیق بھی شامل ہے کہ آیا نمبر نظریہ مستقل اور مکمل ہے۔
حسابی فرکشن / کسر: ایک حصہ ایک جز کے نمائندگی کرتا ہے یا زیادہ عام طور پر مساوی حصوں کی تعداد۔ جب روزمرہ کی انگریزی میں بات کی جاتی ہے تو ، ایک قطعہ بیان کرتا ہے کہ ایک خاص سائز کے کتنے حصے ہیں ، مثال کے طور پر ، ایک آدھ ، آٹھ پچاس ، تین چوتھائی۔ ایک عام ، بے ہودہ یا سادہ سا حصہ ایک سطر کے اوپر دکھائے جانے والے ایک عدد ، اور اس صفر کے نیچے ظاہر ہونے والا ایک غیر صفر فرق پر مشتمل ہوتا ہے۔ ہندسوں اور حرفوں کو بھی ایسے مختلف حصوں میں استعمال کیا جاتا ہے جو عام نہیں ہیں ، بشمول کمپاؤنڈ فرکشن ، پیچیدہ فرکشن اور مخلوط اعداد۔
ریاضی کی تقریب / ریاضی کی تقریب: نمبر تھیوری میں ، ایک ریاضی ، ریاضی یا نمبر نظریاتی فعل زیادہ تر مصنفین کے لئے ہوتا ہے کوئی بھی فنکشن f ( n ) جس کا ڈومین مثبت عدد ہوتا ہے اور جس کی حد پیچیدہ اعداد کا سب سیٹ ہوتی ہے۔ ہارڈی اینڈ رائٹ ان کی تعریف میں یہ تقاضا بھی شامل کرتے ہیں کہ ایک ریاضی کی تقریب " n کی کچھ ریاضی کی خاصیت کا اظہار کرتی ہے"۔
ریاضی کے افعال / ریاضی کی تقریب: نمبر تھیوری میں ، ایک ریاضی ، ریاضی یا نمبر نظریاتی فعل زیادہ تر مصنفین کے لئے ہوتا ہے کوئی بھی فنکشن f ( n ) جس کا ڈومین مثبت عدد ہوتا ہے اور جس کی حد پیچیدہ اعداد کا سب سیٹ ہوتی ہے۔ ہارڈی اینڈ رائٹ ان کی تعریف میں یہ تقاضا بھی شامل کرتے ہیں کہ ایک ریاضی کی تقریب " n کی کچھ ریاضی کی خاصیت کا اظہار کرتی ہے"۔
ریاضی کی نسل / ریاضی کی جینس: ریاضی میں ، الجبری نوع کی ریاضی کی جینس ایک الجبری وکر یا ریمان سطح کی جینس کی کچھ ممکنہ عمومیات میں سے ایک ہے۔
ریاضی کا جغرافیائی_میان / ریاضی – ہندسیاتی مطلب: ریاضی میں ، ریاضی کے two ہندسی اوسط سے دو مثبت اصل نمبر x اور y کی وضاحت کی جاتی ہے۔
ریاضی کی جیومیٹری / ریاضی کا ستادوستی: ریاضی میں ، ریاضی ریاضی تقریبا rough الیگابرک جیومیٹری سے لے کر نمبر تھیوری میں دشواریوں تک کی تکنیک کا استعمال ہوتا ہے۔ ریاضی کا جیومیٹری ڈیوفانٹائن جیومیٹری کے ارد گرد مرکوز ہے ، الجبراic قسموں کے عقلی نکات کا مطالعہ۔
ریاضی گروپ / ریاضی گروپ: ریاضی میں ، ریاضی کا گروپ ایک ایسا گروپ ہوتا ہے جس کو الجبری گروپ کے عددی نکات کے طور پر حاصل کیا جاتا ہے ، مثال کے طور پر وہ تعداد نظریہ میں چکنے والی شکلوں اور دیگر کلاسیکی موضوعات کے ریاضی کی خصوصیات کے مطالعے میں قدرتی طور پر پیدا ہوتے ہیں۔ وہ ریمانیان کی کئی گنا بہت دلچسپ مثالوں کو بھی جنم دیتے ہیں اور اسی وجہ سے امتیازی جغرافیہ اور ٹوپوالوجی میں دلچسپی لیتے ہیں۔ آخر میں ، یہ دونوں عنوانات آٹومورفک شکلوں کے نظریہ میں شامل ہیں جو جدید تعداد کے نظریہ میں بنیادی ہے۔
ریاضی کی نمو / لکیری فنکشن: ریاضی میں ، لکیری فنکشن سے مراد دو الگ الگ لیکن متعلقہ خیالات ہیں۔ کیلکولس اور اس سے وابستہ علاقوں میں ، ایک لکیری فنکشن ایک ایسا فنکشن ہوتا ہے جس کا گراف سیدھی لائن ہوتا ہے ، یعنی ، ڈگری صفر یا ایک کا کثیرالجہتی فعل۔ اس طرح کے لکیری فنکشن کو دوسرے تصور سے ممتاز کرنے کے لئے ، اکثر affine فنکشن استعمال ہوتا ہے۔ لکیری الجبرا ، ریاضیاتی تجزیہ ، اور عملی تجزیہ میں ، ایک لکیری فنکشن ایک لکیری نقشہ ہوتا ہے۔
حسابی ہارمونک_میان / ہندسی مطلب: ریاضی میں ، ہندسی اوسط ایک اوسط یا اوسط ہوتا ہے ، جو ان کی اقدار کی مصنوعات کو استعمال کرکے اعداد کی ایک سیٹ کے مرکزی رجحان یا مخصوص قدر کی نشاندہی کرتا ہے۔ ہندسی وسط کی وضاحت n نمبروں کی مصنوع کی n ویں جڑ کے طور پر کی جاتی ہے ، یعنی x 1 ، x 2 ، ... ، x n اعداد کی ایک سیٹ کے لئے ، ہندسی مطلب کی وضاحت کی جاتی ہے
ریاضی کا درجہ بندی / ریاضی کا درجہ بندی: ریاضیاتی منطق میں ، ریاضی کی درجہ بندی ، ریاضی کے تنظیمی ڈھانچے یا کلین – موسٹوسکی درجہ بندی کچھ فارموں کی درجہ بندی کرتی ہے جو ان کی وضاحت کرنے والے فارمولوں کی پیچیدگی پر مبنی ہوتی ہے۔ کوئی بھی سیٹ جو درجہ بندی حاصل کرتا ہے اسے ریاضی کہا جاتا ہے ۔
ریاضی کا ہائپربولک 14۔ کئی گنا / حسابی ہائپرپولک 3 گنا کئی گنا: ریاضی میں ، زیادہ واضح طور پر گروپ تھیوری اور ہائپربولک جیومیٹری میں ، ریاضیاتی کلینی گروپس کلینین گروپوں کی ایک خاص کلاس ہیں جو کوٹرنین الجبرا میں آرڈروں کا استعمال کرتے ہوئے تعمیر کرتے ہیں۔ وہ ریاضی کے گروپوں کی خاص مثال ہیں۔ ایک ریاضی کا ہائپربولک تین گنا کئی مرتبہ ہائپربولک جگہ کا حص theہ ہے ایک ریاضی کلینین گروپ کے ذریعہ ان کئی گنا میں کچھ خاص طور پر خوبصورت یا قابل ذکر مثالوں شامل ہیں۔
ریاضی کا ہائپربولک_سرفیس / ریاضی کا فوچین گروپ: ریاضی کا فوچیان گروپ فوچیان گروپوں کا ایک خاص طبقہ ہے جو کوٹرنین الجبرا میں آرڈروں کا استعمال کرکے تعمیر کیا گیا تھا۔ وہ ریاضی کے گروپوں کی خاص مثال ہیں۔ ایک ریاضی کے فوچیان گروپ کی ابتدائی مثال ماڈیولر گروپ ہے . وہ ، اور ہائپربولک طیارے پر ان کے عمل سے وابستہ ہائپربولک سطح اکثر فوچیان گروپوں اور ہائپربولک سطحوں کے مابین خاص طور پر باقاعدہ طرز عمل کی نمائش کرتے ہیں۔
ریاضی اگر / ریاضی IF: ریاضی IF بیان ایک تین طرفہ ریاضی کا مشروط بیان ہے جو 1957 میں فورٹرن کے پہلے اجراء میں دیکھا گیا تھا ، اور اس کے بعد کے تمام ورژن ، اور کچھ دیگر پروگرامنگ زبانوں میں ملا ، جیسے فوکل۔ دوسری زبانوں میں منطقی IF بیانات کے برعکس ، فورٹرن بیان تین مختلف شاخوں کی وضاحت کرتا ہے اس پر انحصار کرتا ہے کہ آیا اظہار کا نتیجہ منفی ، صفر ، یا مثبت ہے ، اس ترتیب میں ، لکھا گیا ہے:
ریاضی فن میں ریاضی میں_نوئی_سیکسین / نو ابواب: ریاضی کے فن پر نو بابیں ایک چینی ریاضی کی کتاب ہے ، جو دسویں صدی سے دوسری صدی قبل مسیح کے کئی نسلوں کے اسکالروں پر مشتمل ہے ، اس کا تازہ ترین مرحلہ دوسری صدی عیسوی کا ہے۔ یہ کتاب چین سے ابتدائی طور پر زندہ بچ جانے والی ریاضی کی عبارتوں میں سے ایک ہے ، پہلی کتاب سوان شو شو اور ژوببی سنجنگ ہے ۔ اس میں ریاضی کے بارے میں ایک نقطہ نظر پیش کیا گیا ہے جس میں مسائل کے حل کے سب سے عمومی طریقوں کو تلاش کرنے پر توجہ دی گئی ہے ، جو قدیم یونانی ریاضی دانوں کے لئے عام نقطہ نظر سے متصادم ہوسکتے ہیں ، جنھوں نے محوروں کے ابتدائی مجموعے سے تجاویز کا تخفیف کیا تھا۔
ریاضی میں_فائنٹ_ فیلڈز / فائنائٹ فیلڈ ریاضی: ریاضی میں ، متعدد فیلڈ ریاضی ریاضی اعداد کی فیلڈ کی طرح لامحدود عنصروں والے فیلڈ میں ریاضی کے برعکس ایک متناسب میدان میں ریاضی ہے۔
ریاضی فن پر ریاضی میں_نائن_چھاٹرز / نو ابواب: ریاضی کے فن پر نو بابیں ایک چینی ریاضی کی کتاب ہے ، جو دسویں صدی سے دوسری صدی قبل مسیح کے کئی نسلوں کے اسکالروں پر مشتمل ہے ، اس کا تازہ ترین مرحلہ دوسری صدی عیسوی کا ہے۔ یہ کتاب چین سے ابتدائی طور پر زندہ بچ جانے والی ریاضی کی عبارتوں میں سے ایک ہے ، پہلی کتاب سوان شو شو اور ژوببی سنجنگ ہے ۔ اس میں ریاضی کے بارے میں ایک نقطہ نظر پیش کیا گیا ہے جس میں مسائل کے حل کے سب سے عمومی طریقوں کو تلاش کرنے پر توجہ دی گئی ہے ، جو قدیم یونانی ریاضی دانوں کے لئے عام نقطہ نظر سے متصادم ہوسکتے ہیں ، جنھوں نے محوروں کے ابتدائی مجموعے سے تجاویز کا تخفیف کیا تھا۔
ریاضی کی شدت / چھت کے ماڈل: روف لائن ماڈل ایک بدیہی بصری کارکردگی کا نمونہ ہے جو ایک دیئے گئے کمپیوٹ کارنل یا ملٹی کور ، بہت سے بنیادی ، یا ایکسلریسر پروسیسر فن تعمیرات پر چلنے والی ہارڈ ویئر کی حدود ، اور اصلاح کی ممکنہ فوائد اور ترجیحی کارکردگی کا تخمینہ فراہم کرنے کے لئے استعمال ہوتا ہے۔ محل وقوع ، بینڈوتھ اور متوازی شکل کے مختلف نمونوں کو ایک ہی کارکردگی کے اعداد و شمار میں جوڑ کر ، ماڈل آسان کارکردگی کا اندازہ لگانے کے بجائے حاصل شدہ کارکردگی کے معیار کا اندازہ کرنے کے لئے ایک مؤثر متبادل ثابت ہوسکتا ہے ، کیونکہ یہ عمل درآمد اور دونوں پر بصیرت فراہم کرتا ہے۔ موروثی کارکردگی کی حدود۔
حسابی الٹی / ضرب الٹی: ریاضی میں ، ایک x کے لئے ضرب الٹا یا تکرار ، جس کو 1 / x یا x −1 سے تعبیر کیا جاتا ہے ، ایک ایسی تعداد ہے جو x کے ضرب لگاتے وقت ضرباتی شناخت حاصل کرتا ہے ، 1. کسی ایک حصے a / b کا ضرب الٹا بی / a . اصل اعداد کے ضرب عضب کیلئے ، نمبر کے حساب سے 1 کو تقسیم کریں۔ مثال کے طور پر ، 5 کا باہمی حص oneہ ایک پانچواں ہے ، اور 0.25 کا باہمی حصہ 1 کو 0.25 ، یا 4 سے تقسیم کیا جاتا ہے۔ ایک دوسرے سے ملنے والی افعال ، فعل f ( x ) جو X کو 1 / x کا نقشہ بناتا ہے ، ان میں سے ایک آسان مثال ہے۔ ایک فنکشن جو اس کا اپنا الٹا ہے۔
ریاضی کا جال / جعلی (مجرد سب گروپ): جھوٹ اصول اور ریاضی کے متعلقہ علاقوں میں، ایک مقامی طور پر کمپیکٹ گروپ میں ایک جعلی جائیداد قسیم کی جگہ متناہی غیر تغیر پیمانہ ہے کے ساتھ ایک مجرد ذیلی گروپ ہے. R n کے ذیلی گروپوں کے خصوصی معاملے میں ، یہ پوائنٹس کے وقفے وقفے سے سبسیٹ کی حیثیت سے ایک جالی کے معمول کے ہندسی تصور کے مترادف ہے ، اور جالیوں کی الگ الگ ساختی ڈھانچہ اور تمام جالیوں کی جگہ کی ہندسیاتی نسبتا well اچھی طرح سے سمجھا جاتا ہے۔
ریاضی کا سیکھنے_ڈیسڈر / ڈیسکلکولیا: ڈیسکلکولیا ایک ایسی معذوری ہے جس کے نتیجے میں ریاضی کے سیکھنے یا ریاضی کو سمجھنے میں دشواری ہوتی ہے جیسے نمبروں کو سمجھنے میں دشواری ، نمبروں کو جوڑ توڑ کرنے کا طریقہ سیکھنا ، ریاضی کے حساب کتاب کرنا اور ریاضی میں حقائق سیکھنا۔ یہ کبھی کبھی غیر رسمی طور پر "ریاضی ڈسلیسیا" کے نام سے جانا جاتا ہے ، حالانکہ یہ گمراہ کن ہوسکتا ہے کیونکہ ڈیسلیسیا ڈسکلکولیا سے مختلف حالت ہے۔
ریاضی کی بائیں سمت / ریاضی کی شفٹ: کمپیوٹر پروگرامنگ میں ، ریاضی کی شفٹ شفٹ آپریٹر ہوتی ہے ، جسے کبھی کبھی دستخط شدہ شفٹ بھی کہتے ہیں ۔ دو بنیادی اقسام ریاضی کی بائیں شفٹ اور ریاضی کی دائیں شفٹ ہیں ۔ بائنری نمبروں کے لئے یہ تھوڑا سا آپریشن ہے جو اس کے نقاط کے تمام بٹس کو تبدیل کرتا ہے۔ اوپیرینڈ میں ہر بٹ آسانی سے بٹ پوزیشنوں کی ایک دی گئی بڑی تعداد میں منتقل ہوجاتا ہے ، اور خالی بٹ پوزیشنز پُر ہوجاتی ہیں۔ تمام 0s سے پُر ہونے کی بجائے ، منطقی شفٹ کی طرح ، جب دائیں طرف شفٹ ہوتا ہے تو ، بائیں بازو کو دوبارہ تیار کیا جاتا ہے تمام خالی آسامیوں کو پُر کریں۔
ریاضی کی منطق_ یونیت / ریاضی کی منطق یونٹ: کمپیوٹنگ میں ، ایک ریاضی کا منطق یونٹ (ALU) ایک مشترکہ ڈیجیٹل سرکٹ ہے جو عددی بائنری نمبروں پر ریاضی اور بٹویس آپریشن انجام دیتا ہے۔ یہ فلوٹنگ پوائنٹ یونٹ (FPU) کے برعکس ہے ، جو فلوٹنگ پوائنٹ نمبرز پر کام کرتا ہے۔ یہ کمپیوٹنگ سرکٹوں کی بہت سی اقسام کا بنیادی عمارت ہے ، جس میں کمپیوٹروں کی سنٹرل پروسیسنگ یونٹ (سی پی یو) ، ایف پی یو ، اور گرافکس پروسیسنگ یونٹ (جی پی یو) شامل ہیں۔
ریاضیاتی منطق_ یونٹ٪ 5C / ریاضی کی منطق یونٹ: کمپیوٹنگ میں ، ایک ریاضی کا منطق یونٹ (ALU) ایک مشترکہ ڈیجیٹل سرکٹ ہے جو عددی بائنری نمبروں پر ریاضی اور بٹویس آپریشن انجام دیتا ہے۔ یہ فلوٹنگ پوائنٹ یونٹ (FPU) کے برعکس ہے ، جو فلوٹنگ پوائنٹ نمبرز پر کام کرتا ہے۔ یہ کمپیوٹنگ سرکٹوں کی بہت سی اقسام کا بنیادی عمارت ہے ، جس میں کمپیوٹروں کی سنٹرل پروسیسنگ یونٹ (سی پی یو) ، ایف پی یو ، اور گرافکس پروسیسنگ یونٹ (جی پی یو) شامل ہیں۔
ریاضی کا منطق کمپیوٹنگ میں ، ایک ریاضی کا منطق یونٹ (ALU) ایک مشترکہ ڈیجیٹل سرکٹ ہے جو عددی بائنری نمبروں پر ریاضی اور بٹویس آپریشن انجام دیتا ہے۔ یہ فلوٹنگ پوائنٹ یونٹ (FPU) کے برعکس ہے ، جو فلوٹنگ پوائنٹ نمبرز پر کام کرتا ہے۔ یہ کمپیوٹنگ سرکٹوں کی بہت سی اقسام کا بنیادی عمارت ہے ، جس میں کمپیوٹروں کی سنٹرل پروسیسنگ یونٹ (سی پی یو) ، ایف پی یو ، اور گرافکس پروسیسنگ یونٹ (جی پی یو) شامل ہیں۔
ریاضی مشین / پاسکل کیلکولیٹر: پاسکل کا کیلکولیٹر ایک مکینیکل کیلکولیٹر ہے جسے 17 ویں صدی کے وسط میں بلیس پاسکل نے ایجاد کیا تھا۔ پاسکل کو روین میں ٹیکسوں کے نگراں نگران کی حیثیت سے اپنے والد کے کام کے ذریعہ درکار حساب کتاب کے حساب سے ایک کیلکولیٹر تیار کرنا تھا۔ اس نے مشین کو دو نمبروں کو براہ راست شامل کرنے اور منہا کرنے کے لئے اور بار بار اضافے یا گھٹاؤ کے ذریعہ ضرب اور تقسیم کرنے کے لئے ڈیزائن کیا۔
ریاضی کا مطلب / ریاضی کا مطلب: ریاضی اور اعدادوشمار میں ، ریاضی کا مطلب ، یا محض اسباب یا اوسط ، مجموعوں میں اعداد کی گنتی کے حساب سے تقسیم کردہ اعداد کے مجموعے کا مجموعہ ہے۔ یہ مجموعہ اکثر کسی تجربے یا مشاہداتی مطالعے کے نتائج کا ایک سیٹ ہوتا ہے ، یا اکثر کسی سروے کے نتائج کا ایک سیٹ ہوتا ہے۔ ریاضی اور اعدادوشمار کے کچھ سیاق و سباق میں "ریاضی کا مطلب" کی اصطلاح کو ترجیح دی جاتی ہے ، کیوں کہ اس سے اس کو دوسرے ذرائع سے ممتاز کرنے میں مدد ملتی ہے ، جیسے ہندسی مطلب اور ہارمونک وسیلہ۔
ریاضی کا مطلب-ہندسی_میان_فاقت / ریاضی اور ہندسی ذرائع کی عدم مساوات: ریاضی میں ، ریاضی اور ہندسی ذرائع کی عدم مساوات ، یا زیادہ مختصر طور پر AM – GM عدم مساوات ، بتاتا ہے کہ غیر منفی اصل تعداد کی ایک فہرست کا ریاضی کا مطلب ایک ہی فہرست کے ہندسی مطلب سے زیادہ یا مساوی ہے۔ اور مزید یہ کہ دونوں ذرائع برابر ہیں اگر اور صرف اس صورت میں جب فہرست میں ہر تعداد ایک جیسی ہو۔
ریاضی کے معیار / نورم (ریاضی): ریاضی میں ، ایک معمول ایک حقیقی یا پیچیدہ ویکٹر خلا سے لے کر غیر منقطع اصلی تعداد تک کا ایک ایسا فعل ہوتا ہے جو کچھ طریقوں سے ابتداء سے فاصلے کی طرح برتاؤ کرتا ہے: یہ اسکیلنگ سے بدلا جاتا ہے ، مثلث کی عدم مساوات کی ایک شکل مانتا ہے ، اور صرف صفر پر ہے اصل خاص طور پر ، اصل سے ویکٹر کا یکلیڈین فاصلہ ایک معمول ہے ، جسے Euclidean نورم یا 2-نوروم کہا جاتا ہے ، جسے اپنے ساتھ ویکٹر کے اندرونی مصنوع کا مربع جڑ بھی قرار دیا جاسکتا ہے۔
حسابی نمبر / ریاضی نمبر: نمبر نظریہ میں ، ایک ریاضی کی تعداد ایک عددی ہوتی ہے جس کے ل its اس کے مثبت طلاق دینے والوں کی اوسط بھی ایک عدد اعداد ہوتی ہے۔ مثال کے طور پر ، 6 ایک ریاضی کی تعداد ہے کیونکہ اس کے طلاق دینے والوں کی اوسط ہے
ریاضی کا_ا_مرڈر / ریاضی کا ریاضی: ریاضی کا ریاضی 1991 کی سوویت کرائم فلم ہے جس کا ہدایتکار دمتری سویٹو زاروف ہے۔
ریاضی کی_ابیلیئن_واورائٹس / ریاضی کی مختلف قسم کے ریاضی: ریاضی میں ، ابلیئن اقسام کا ریاضی ایک ابلیئن اقسام کے نمبر تھیوری کا مطالعہ ہوتا ہے ، یا ابیلیئن اقسام کے کنبے کا۔ یہ پیئری ڈی فیرمٹ کے مطالعے پر واپس آجاتا ہے جسے اب بیضوی منحنی خطوط کے طور پر پہچانا جاتا ہے۔ اور نتائج اور تخمینوں کے لحاظ سے ریاضی کے جیومیٹری کا ایک بہت ہی اہم علاقہ بن گیا ہے۔ ان میں سے بیشتر ابلیسی قسم A کے لئے متعدد فیلڈ K سے پوجا ہوسکتے ہیں۔ یا زیادہ عام طور پر۔
ابیلیئن قسموں کے ریاضی کا_یلیپٹیک_کورو / ریاضی: ریاضی میں ، ابلیئن اقسام کا ریاضی ایک ابلیئن اقسام کے نمبر تھیوری کا مطالعہ ہوتا ہے ، یا ابیلیئن اقسام کے کنبے کا۔ یہ پیئری ڈی فیرمٹ کے مطالعے پر واپس آجاتا ہے جسے اب بیضوی منحنی خطوط کے طور پر پہچانا جاتا ہے۔ اور نتائج اور تخمینوں کے لحاظ سے ریاضی کے جیومیٹری کا ایک بہت ہی اہم علاقہ بن گیا ہے۔ ان میں سے بیشتر ابلیسی قسم A کے لئے متعدد فیلڈ K سے پوجا ہوسکتے ہیں۔ یا زیادہ عام طور پر۔
ابیلیئن قسموں کے ریاضی کا_یلیپٹک_کوروز / ریاضی ریاضی میں ، ابلیئن اقسام کا ریاضی ایک ابلیئن اقسام کے نمبر تھیوری کا مطالعہ ہوتا ہے ، یا ابیلیئن اقسام کے کنبے کا۔ یہ پیئری ڈی فیرمٹ کے مطالعے پر واپس آجاتا ہے جسے اب بیضوی منحنی خطوط کے طور پر پہچانا جاتا ہے۔ اور نتائج اور تخمینوں کے لحاظ سے ریاضی کے جیومیٹری کا ایک بہت ہی اہم علاقہ بن گیا ہے۔ ان میں سے بیشتر ابلیسی قسم A کے لئے متعدد فیلڈ K سے پوجا ہوسکتے ہیں۔ یا زیادہ عام طور پر۔
ریاضی کا_فائنٹ_ فیلڈز / فائنائٹ فیلڈ ریاضی: ریاضی میں ، متعدد فیلڈ ریاضی ریاضی اعداد کی فیلڈ کی طرح لامحدود عنصروں والے فیلڈ میں ریاضی کے برعکس ایک متناسب میدان میں ریاضی ہے۔
ریاضی / معمول کے ریاضی کا ریاضی: سیٹ تھیوری کے ریاضی کے میدان میں ، عام ریاضی میں عام تعداد میں تین معمول کی کارروائیوں کو بیان کیا جاتا ہے: اضافہ ، ضرب اور کثرت۔ ہر ایک کی بنیادی طور پر دو مختلف طریقوں سے تعریف کی جاسکتی ہے: یا تو ایک واضح اچھی طرح سے ترتیب دی گئی سیٹ تیار کرکے جو آپریشن کے نتائج کی نمائندگی کرتی ہے یا عبوری تکرار کا استعمال کرکے۔ کینٹر کا نارمل فارم آرڈینلز لکھنے کا ایک معیاری طریقہ فراہم کرتا ہے۔ معمول کی ان معمولی کارروائیوں کے علاوہ ، آرڈینلز کی قدرتی ریاضی اور نمبر آپریشن بھی موجود ہیں۔
ریاضی کے آپریشن / ریاضی: ریاضی کی ریاضی کی ایک شاخ ہے جو اعداد کے مطالعہ پر مشتمل ہے ، خاص طور پر ان پر روایتی کارروائیوں کی خصوصیات کے علاوہ — اس کے علاوہ ، گھٹائو ، ضرب ، تقسیم ، کفارہ اور جڑوں کی کھوج۔ ریاضی شماری نمبر تھیوری کا ایک ابتدائی حصہ ہے ، اور عدد نظریہ کو الجبرا ، جیومیٹری اور تجزیہ کے ساتھ جدید ریاضی کی اعلی سطحی تقسیم میں سے ایک سمجھا جاتا ہے۔ ریاضی اور اعلی ریاضی کی اصطلاحیں 20 ویں صدی کے آغاز تک نمبر نظریہ کے مترادفات کے طور پر استعمال ہوتی تھیں اور بعض اوقات اب بھی عدد نظریہ کے وسیع حصے کا حوالہ دیتے ہیں۔
ریاضی کے عمل / ریاضی: ریاضی کی ریاضی کی ایک شاخ ہے جو اعداد کے مطالعہ پر مشتمل ہے ، خاص طور پر ان پر روایتی کارروائیوں کی خصوصیات کے علاوہ — اس کے علاوہ ، گھٹائو ، ضرب ، تقسیم ، کفارہ اور جڑوں کی کھوج۔ ریاضی شماری نمبر تھیوری کا ایک ابتدائی حصہ ہے ، اور عدد نظریہ کو الجبرا ، جیومیٹری اور تجزیہ کے ساتھ جدید ریاضی کی اعلی سطحی تقسیم میں سے ایک سمجھا جاتا ہے۔ ریاضی اور اعلی ریاضی کی اصطلاحیں 20 ویں صدی کے آغاز تک نمبر نظریہ کے مترادفات کے طور پر استعمال ہوتی تھیں اور بعض اوقات اب بھی عدد نظریہ کے وسیع حصے کا حوالہ دیتے ہیں۔
ریاضی کا آپریٹر / ریاضی: ریاضی کی ریاضی کی ایک شاخ ہے جو اعداد کے مطالعہ پر مشتمل ہے ، خاص طور پر ان پر روایتی کارروائیوں کی خصوصیات کے علاوہ — اس کے علاوہ ، گھٹائو ، ضرب ، تقسیم ، کفارہ اور جڑوں کی کھوج۔ ریاضی شماری نمبر تھیوری کا ایک ابتدائی حصہ ہے ، اور عدد نظریہ کو الجبرا ، جیومیٹری اور تجزیہ کے ساتھ جدید ریاضی کی اعلی سطحی تقسیم میں سے ایک سمجھا جاتا ہے۔ ریاضی اور اعلی ریاضی کی اصطلاحیں 20 ویں صدی کے آغاز تک نمبر نظریہ کے مترادفات کے طور پر استعمال ہوتی تھیں اور بعض اوقات اب بھی عدد نظریہ کے وسیع حصے کا حوالہ دیتے ہیں۔
ریاضی کے آپریٹرز / ریاضی: ریاضی کی ریاضی کی ایک شاخ ہے جو اعداد کے مطالعہ پر مشتمل ہے ، خاص طور پر ان پر روایتی کارروائیوں کی خصوصیات کے علاوہ — اس کے علاوہ ، گھٹائو ، ضرب ، تقسیم ، کفارہ اور جڑوں کی کھوج۔ ریاضی شماری نمبر تھیوری کا ایک ابتدائی حصہ ہے ، اور عدد نظریہ کو الجبرا ، جیومیٹری اور تجزیہ کے ساتھ جدید ریاضی کی اعلی سطحی تقسیم میں سے ایک سمجھا جاتا ہے۔ ریاضی اور اعلی ریاضی کی اصطلاحیں 20 ویں صدی کے آغاز تک نمبر نظریہ کے مترادفات کے طور پر استعمال ہوتی تھیں اور بعض اوقات اب بھی عدد نظریہ کے وسیع حصے کا حوالہ دیتے ہیں۔
ریاضی کے اوور فلو / انٹیجر اوور فلو: کمپیوٹر پروگرامنگ میں ، ایک انٹیجر اوور فلو اس وقت ہوتا ہے جب ریاضی کے عمل نے ایک عددی قیمت پیدا کرنے کی کوشش کی جو حد سے باہر ہو جس کی نمائندگی ہندسوں کی ایک تعداد سے کی جاسکے۔
حسابی پی پی اڈک_ ایل فنکشن / پی ایڈک ایل فنکشن: ریاضی میں ، p -adic zeta فنکشن ، یا زیادہ عام طور پر p -adic L -function ، ایک تقریب ہے جو Riemann zeta فنکشن ، یا زیادہ عام L- فنکشن کے مطابق ہے ، لیکن جس کا ڈومین اور ہدف p-adic ہے ۔ مثال کے طور پر، ڈومین P -adic integers کے Z P، ایک profinite P -group، یا Galois نمائندگی کی ایک P -adic خاندان ہو سکتا ہے، اور تصویر P -adic اعداد Q P یا اس الجبری بندش ہو سکتا ہے.
ریاضی کی صحت سے متعلق / اہم شخصیات: پوزیشن کی نشاندہی میں کسی بڑی تعداد کے اہم اعداد و شمار میں ایسے ہندسے ہوتے ہیں جو قابل اعتبار ہیں اور کسی چیز کی مقدار کی نشاندہی کرنے کے لئے بالکل ضروری ہیں۔ اگر کسی عدد کی پیمائش کے نتیجے کو ظاہر کرنے والے پیمائش ریزولوشن کے ذریعہ منظور کردہ ہندسوں سے زیادہ ہندسے رکھتے ہیں تو ، پیمائش کی قرارداد کے ذریعہ اجازت دی گئی ہندسے قابل اعتماد ہیں لہذا صرف یہ اہم اعداد و شمار ہوسکتے ہیں۔ مثال کے طور پر ، اگر لمبائی کی پیمائش 114.8 ملی میٹر ہوتی ہے جبکہ پیمائش میں استعمال ہونے والے حکمران پر نشان کے درمیان سب سے چھوٹا وقفہ 1 ملی میٹر ہوتا ہے ، تو پہلے تین ہندسے صرف قابل اعتماد ہوتے ہیں لہذا اہم اعداد و شمار ہوسکتے ہیں۔ ان ہندسوں میں ، آخری ہندسے میں غیر یقینی صورتحال موجود ہے لیکن یہ بھی ایک اہم اعداد و شمار کے طور پر سمجھا جاتا ہے کیونکہ ایسے ہندسوں کو جو غیر یقینی لیکن قابل اعتماد ہیں ، کو اہم اعداد و شمار سمجھا جاتا ہے۔ ایک اور مثال 2.98 L کی حجم کی پیمائش ہے جس میں ± 0.05 L کی غیر یقینی صورتحال ہے۔ اصل حجم کہیں کہیں 2.93 L اور 3.03 L کے درمیان ہے۔ یہاں تک کہ اگر تینوں ہندسے یقینی لیکن قابل اعتبار نہیں ہیں کیونکہ یہ قابل قبول غیر یقینی صورتحال کے ساتھ اصل حجم کی نشاندہی کرتی ہے . تو ، یہ اہم شخصیات ہیں۔
ریاضی کی ترقی / ریاضی کی ترقی: ایک ریاضی کی ترقی یا ریاضی کی ترتیب نمبروں کا ایک ایسا تسلسل ہے کہ لگاتار شرائط کے مابین فرق مستقل رہتا ہے۔ مثال کے طور پر ، تسلسل 5 ، 7 ، 9 ، 11 ، 13 ، 15 ،۔ .. ایک ریاضی کی ترقی ہے جو 2 کے عام فرق کے ساتھ ہے۔
ریاضی کی پیشرفت_ گیم / ریاضی کی ترقی کا کھیل: ریاضی کا ترقی پسندی کا کھیل ایک کھیلی کھیل ہے جہاں دو کھلاڑی باری باری نمبریں منتخب کرتے ہیں ، ایک دیئے گئے سائز کی مکمل ریاضی کی نشوونما پر قبضہ کرنے کی کوشش کرتے ہیں۔
ریاضی کی پیشرفت / ریاضی کی ترقی: ایک ریاضی کی ترقی یا ریاضی کی ترتیب نمبروں کا ایک ایسا تسلسل ہے کہ لگاتار شرائط کے مابین فرق مستقل رہتا ہے۔ مثال کے طور پر ، تسلسل 5 ، 7 ، 9 ، 11 ، 13 ، 15 ،۔ .. ایک ریاضی کی ترقی ہے جو 2 کے عام فرق کے ساتھ ہے۔
ریاضی کی خصوصیات / رنگ (ریاضی): ریاضی میں ، حلقے الجبراicک ڈھانچے ہوتے ہیں جو کھیتوں کو عام کرتے ہیں: ضرب بدلنے کی ضرورت نہیں ہے اور ضرب الٹی وجود کی ضرورت نہیں ہے۔ دوسرے لفظوں میں ، ایک انگوٹی ایک سیٹ ہے جو دو بائنری آپریشنوں سے لیس ہے جو اطمینان بخش خصوصیات کے ساتھ ملتی ہے اور عددی اعداد کے ضوابط سے ملتی ہے۔ رنگ عناصر عددی نمبر یا عددی پیچیدہ اعداد ہوسکتے ہیں ، لیکن وہ غیر عددی اشیاء بھی ہوسکتے ہیں جیسے متعدد ، مربع میٹرکس ، افعال ، اور پاور سیریز۔
ریاضی کی کمی / ریاضی کی درجہ بندی: ریاضیاتی منطق میں ، ریاضی کی درجہ بندی ، ریاضی کے تنظیمی ڈھانچے یا کلین – موسٹوسکی درجہ بندی کچھ فارموں کی درجہ بندی کرتی ہے جو ان کی وضاحت کرنے والے فارمولوں کی پیچیدگی پر مبنی ہوتی ہے۔ کوئی بھی سیٹ جو درجہ بندی حاصل کرتا ہے اسے ریاضی کہا جاتا ہے ۔
ریاضی کی واپسی / واپسی کی شرح: فنانس میں ، واپسی ایک سرمایہ کاری پر منافع ہے۔ اس میں سرمایہ کاری کی قدر میں کوئی تبدیلی ، اور / یا نقد بہاؤ شامل ہوتا ہے جو سرمایہ کار کو اس سرمایہ کاری سے حاصل ہوتا ہے ، جیسے سود کی ادائیگی ، کوپن ، نقد منافع ، اسٹاک کے منافع یا مشتق یا تشکیل شدہ مصنوع کی ادائیگی۔ اس کو یا تو مطلق شرائط میں یا سرمایہ کاری کی گئی رقم کی فیصد کے طور پر ناپا جاسکتا ہے۔ مؤخر الذکر کو انعقاد کی مدت کی واپسی بھی کہا جاتا ہے۔
ریاضی کی دائیں_شافٹ / ریاضی کی شفٹ: کمپیوٹر پروگرامنگ میں ، ریاضی کی شفٹ شفٹ آپریٹر ہوتی ہے ، جسے کبھی کبھی دستخط شدہ شفٹ بھی کہتے ہیں ۔ دو بنیادی اقسام ریاضی کی بائیں شفٹ اور ریاضی کی دائیں شفٹ ہیں ۔ بائنری نمبروں کے لئے یہ تھوڑا سا آپریشن ہے جو اس کے نقاط کے تمام بٹس کو تبدیل کرتا ہے۔ اوپیرینڈ میں ہر بٹ آسانی سے بٹ پوزیشنوں کی ایک دی گئی بڑی تعداد میں منتقل ہوجاتا ہے ، اور خالی بٹ پوزیشنز پُر ہوجاتی ہیں۔ تمام 0s سے پُر ہونے کی بجائے ، منطقی شفٹ کی طرح ، جب دائیں طرف شفٹ ہوتا ہے تو ، بائیں بازو کو دوبارہ تیار کیا جاتا ہے تمام خالی آسامیوں کو پُر کریں۔
ریاضی کی انگوٹی / ریاضی کی انگوٹھی: الجبرا میں ، ایک بدلنے والی رنگ R کو ریاضی سمجھا جاتا ہے اگر مندرجہ ذیل مساوی شرائط میں سے کسی میں یہ موجود ہے: لوکلائزیشن R پر ہر ایک زیادہ سے زیادہ مثالی کے لئے ایک غیر عسکری رنگ ہے R کے تمام نظریات کے لئے ، اور ، تمام نظریات کے لئے ، اور ،
ریاضی کی رسی / ریاضی کی رسی: ریاضی کا رسی ، یا گرہ لگا ہوا رسی ، قرون وسطی میں وسیع پیمانے پر استعمال ہونے والے ریاضی کا آلہ تھا جسے بہت سارے ریاضی اور جغرافیائی مسائل کو حل کرنے کے لئے استعمال کیا جاسکتا ہے۔
ریاضی اسکیم / اراکیلوف تھیوری: ریاضی میں ، اراکیلوف نظریہ ڈیوفانٹائن جیومیٹری کا ایک نقطہ نظر ہے ، جس کا نام سورن ارکیلوف رکھا گیا ہے۔ یہ اعلی طول و عرض میں ڈیوفانٹائن مساوات کا مطالعہ کرنے کے لئے استعمال ہوتا ہے۔
ریاضی کا سیمی گروپ / خلاصہ تجزیاتی تعداد کا نظریہ: خلاصہ تجزیاتی نمبر تھیوری ریاضی کی ایک شاخ ہے جو کلاسیکی تجزیاتی نمبر تھیوری کے نظریات اور تراکیب لیتا ہے اور مختلف ریاضی کے مختلف شعبوں پر ان کا اطلاق کرتا ہے۔ کلاسیکی پرائم نمبر کا نظریہ ایک پروٹو ٹائپیکل مثال کے طور پر کام کرتا ہے ، اور اسماٹومیٹک تقسیم کے نتائج کو خلاصہ کرنے پر زور دیا جاتا ہے۔ یہ نظریہ بیسویں صدی میں جان نوپفماچر اور آرن بیرلنگ جیسے ریاضی دانوں نے ایجاد اور تیار کیا تھا۔
ریاضی کی ترتیب / ریاضی کی ترقی: ایک ریاضی کی ترقی یا ریاضی کی ترتیب نمبروں کا ایک ایسا تسلسل ہے کہ لگاتار شرائط کے مابین فرق مستقل رہتا ہے۔ مثال کے طور پر ، تسلسل 5 ، 7 ، 9 ، 11 ، 13 ، 15 ،۔ .. ایک ریاضی کی ترقی ہے جو 2 کے عام فرق کے ساتھ ہے۔
ریاضی کی سیریز / ریاضی کی ترقی: ایک ریاضی کی ترقی یا ریاضی کی ترتیب نمبروں کا ایک ایسا تسلسل ہے کہ لگاتار شرائط کے مابین فرق مستقل رہتا ہے۔ مثال کے طور پر ، تسلسل 5 ، 7 ، 9 ، 11 ، 13 ، 15 ،۔ .. ایک ریاضی کی ترقی ہے جو 2 کے عام فرق کے ساتھ ہے۔
حسابی سیٹ / ریاضی کا سیٹ: ریاضیاتی منطق میں ، ریاضی کا ایک مجموعہ قدرتی اعداد کا ایک مجموعہ ہوتا ہے جس کی وضاحت پہلے آرڈر پیانو ریاضی کے فارمولے سے کی جا سکتی ہے۔ ریاضی کے سیٹ کو حسابی درجہ بندی کے ذریعہ درجہ بندی کیا جاتا ہے۔
ریاضی کی شفٹ / ریاضی کی شفٹ: کمپیوٹر پروگرامنگ میں ، ریاضی کی شفٹ شفٹ آپریٹر ہوتی ہے ، جسے کبھی کبھی دستخط شدہ شفٹ بھی کہتے ہیں ۔ دو بنیادی اقسام ریاضی کی بائیں شفٹ اور ریاضی کی دائیں شفٹ ہیں ۔ بائنری نمبروں کے لئے یہ تھوڑا سا آپریشن ہے جو اس کے نقاط کے تمام بٹس کو تبدیل کرتا ہے۔ اوپیرینڈ میں ہر بٹ آسانی سے بٹ پوزیشنوں کی ایک دی گئی بڑی تعداد میں منتقل ہوجاتا ہے ، اور خالی بٹ پوزیشنز پُر ہوجاتی ہیں۔ تمام 0s سے پُر ہونے کی بجائے ، منطقی شفٹ کی طرح ، جب دائیں طرف شفٹ ہوتا ہے تو ، بائیں بازو کو دوبارہ تیار کیا جاتا ہے تمام خالی آسامیوں کو پُر کریں۔
حسابی شارٹ کٹ / ذہنی حساب: ذہنی حساب کتاب ریاضی کے حساب کتابوں پر مشتمل ہوتا ہے جس میں صرف انسانی دماغ استعمال ہوتا ہے جس میں کسی بھی چیز کی فراہمی یا آلات جیسے کیلکولیٹر کی مدد نہیں کی جاتی ہے۔ جب کمپیوٹنگ ٹولز دستیاب نہیں ہوتے ہیں تو لوگ ذہنی حساب کتاب کا استعمال کرتے ہیں ، جب یہ حساب کتاب کے دوسرے ذرائع سے کہیں زیادہ تیز ہوتا ہے یا یہاں تک کہ مسابقتی سیاق و سباق میں۔ ذہنی حساب کتاب میں اکثر مخصوص قسم کی پریشانیوں کے لئے وضع کردہ مخصوص تکنیک کا استعمال شامل ہوتا ہے۔ ذہنی حساب کتاب کرنے کی غیر معمولی اعلی صلاحیت رکھنے والے افراد کو ذہنی کیلکولیٹر یا بجلی کا کیلکولیٹر کہتے ہیں۔
حسابی شارٹ کٹ / ذہنی حساب: ذہنی حساب کتاب ریاضی کے حساب کتابوں پر مشتمل ہوتا ہے جس میں صرف انسانی دماغ استعمال ہوتا ہے جس میں کسی بھی چیز کی فراہمی یا آلات جیسے کیلکولیٹر کی مدد نہیں کی جاتی ہے۔ جب کمپیوٹنگ ٹولز دستیاب نہیں ہوتے ہیں تو لوگ ذہنی حساب کتاب کا استعمال کرتے ہیں ، جب یہ حساب کتاب کے دوسرے ذرائع سے کہیں زیادہ تیز ہوتا ہے یا یہاں تک کہ مسابقتی سیاق و سباق میں۔ ذہنی حساب کتاب میں اکثر مخصوص قسم کی پریشانیوں کے لئے وضع کردہ مخصوص تکنیک کا استعمال شامل ہوتا ہے۔ ذہنی حساب کتاب کرنے کی غیر معمولی اعلی صلاحیت رکھنے والے افراد کو ذہنی کیلکولیٹر یا بجلی کا کیلکولیٹر کہتے ہیں۔
ریاضی کی آواز / آواز: منطق میں، زیادہ واضح طور نگمناتمک استدلال میں، ایک دلیل آواز تو یہ شکل میں دونوں درست ہے اور اس کے احاطے سچ ہو جاتا ہے. ریاضی کی منطق میں بھی صوفیت کا ایک متعلقہ معنی ہے ، جس میں منطقی نظام مستحکم ہے اگر اور صرف اس صورت میں جب ہر فارمولا جو سسٹم میں ثابت ہوسکتا ہے اس نظام کی اصطلاحات کے حوالے سے منطقی طور پر درست ہے۔
ریاضی سرپل / آرچیمیئن سرپل: آرچیمیئن سرپل ایک سرپل ہے جسے تیسری صدی قبل مسیح کے یونانی ریاضی دان آرکیڈیڈس کے نام دیا گیا ہے۔ یہ ایک مقام کے وقت کے ساتھ مقامات سے مطابقت رکھنے والا یہ لوکس ہے جو ایک مستحکم نقطہ سے مستقل رفتار کے ساتھ ایک لائن کے ساتھ آگے بڑھتا ہے جو مستحکم کونیی کی رفتار کے ساتھ گھومتا ہے۔ مساوی طور پر ، قطبی نقاط ( r ، θ ) میں اس مساوات کے ذریعہ بیان کیا جاسکتا ہے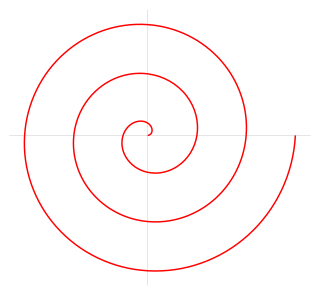
حسابی سب گروپ / ریاضی گروپ: ریاضی میں ، ریاضی کا گروپ ایک ایسا گروپ ہوتا ہے جس کو الجبری گروپ کے عددی نکات کے طور پر حاصل کیا جاتا ہے ، مثال کے طور پر وہ تعداد نظریہ میں چکنے والی شکلوں اور دیگر کلاسیکی موضوعات کے ریاضی کی خصوصیات کے مطالعے میں قدرتی طور پر پیدا ہوتے ہیں۔ وہ ریمانیان کی کئی گنا بہت دلچسپ مثالوں کو بھی جنم دیتے ہیں اور اسی وجہ سے امتیازی جغرافیہ اور ٹوپوالوجی میں دلچسپی لیتے ہیں۔ آخر میں ، یہ دونوں عنوانات آٹومورفک شکلوں کے نظریہ میں شامل ہیں جو جدید تعداد کے نظریہ میں بنیادی ہے۔
ریاضی کی رقم / ریاضی کی ترقی: ایک ریاضی کی ترقی یا ریاضی کی ترتیب نمبروں کا ایک ایسا تسلسل ہے کہ لگاتار شرائط کے مابین فرق مستقل رہتا ہے۔ مثال کے طور پر ، تسلسل 5 ، 7 ، 9 ، 11 ، 13 ، 15 ،۔ .. ایک ریاضی کی ترقی ہے جو 2 کے عام فرق کے ساتھ ہے۔
ریاضی کی سطح / ریاضی کی سطح: ریاضی میں ، ڈیڈکائنڈ ڈومین R کے اوپر ایک قطعہ کی سطح جس میں فکشن فیلڈ ہے ایک ہندسی اشیا ہے جس کا ایک روایتی جہت ہے ، اور ایک دوسرا جہت جو پرائمس کی بے حسی سے فراہم کردہ ہے۔ جب R عددی زیڈ کی انگوٹھی ہوتا ہے تو ، اس بصیرت کا انحصار بنیادی مثالی اسپیکٹرم اسپیس ( Z ) پر ہوتا ہے جو کسی لکیر کے مترادف ہوتا ہے۔ ریاضی کی سطحیں قدرتی طور پر ڈیوفانٹائن جیومیٹری میں پیدا ہوتی ہیں ، جب K کے اوپر بیان کردہ الجبری وکر کے بارے میں سوچا جاتا ہے کہ کھیتوں R / P میں کمی واقع ہوتی ہے ، جہاں P تقریبا R تمام P کے لئے R کا ایک مثالی نمونہ ہے۔ اور یہ واضح کرنے میں مددگار ہیں کہ جب R / P کو کم کرنے کے عمل کے بارے میں کیا ہونا چاہئے جب سب سے زیادہ آسان طریقہ سمجھ میں نہیں آتا ہے۔
ریاضی کی ٹوپیولوجی / ریاضی کی ٹوپوالوجی: ریاضی کا ٹوپوالوجی ریاضی کا ایک ایسا شعبہ ہے جو الجبرایک نمبر تھیوری اور ٹوپولوجی کا امتزاج ہے۔ یہ تعداد والے فیلڈز اور بند ، مستشرق 3 گنا کئی گناوں کے مابین مشابہت قائم کرتا ہے۔
ریاضی کا مثلث_گروپ / کوکسٹر – ڈینکن آریھ: جیومیٹری میں ، ایک کاکسٹر – ڈِنکن آریھ ایک گراف ہے جس میں عددی طور پر لیبل لگے ہوئے کناروں کے ساتھ آئینہ جمع کرنے کے مابین مقامی تعلقات کی نمائندگی کی جاتی ہے۔ اس میں کلیڈیوسکوپک تعمیر کی وضاحت کی گئی ہے: ہر گراف "نوڈ" آئینے کی نمائندگی کرتا ہے اور شاخ سے منسلک لیبل دو آئینے کے درمیان ہیڈرل اینگل آرڈر کو انکوڈ کرتا ہے ، یعنی جس مقدار کے ذریعہ عکاس طیاروں کے درمیان زاویہ ضرب ہوسکتی ہے 180 ڈگری بغیر لیبل لگا شاخ آرڈر 3 کی واضح نمائندگی کرتی ہے۔
حسابی انڈر فلو / ریاضی کا انڈر فلو: ریاضی انڈر فلو کی اصطلاح ایک کمپیوٹر پروگرام میں ایک ایسی حالت ہے جہاں حساب کے نتیجے میں کمپیوٹر اس کے مرکزی پروسیسنگ یونٹ (سی پی یو) کی یادداشت میں دراصل نمائندگی کرنے والے مقابلے میں بہت کم مطلق قدر کی حیثیت رکھتا ہے۔
ریاضی کی مختلف اقسام / ریاضی کی مختلف اقسام: ریاضی میں ، ریاضی میں مختلف نوعیت کا تعلق ہرمیئن سمتار جگہ کی ہے جو وابستہ الجبرک جھوٹے گروپ کے ریاضی کے ایک گروہوں کے ذریعہ ہوتا ہے۔
ریاضی کی مختلف اقسام / ریاضی کی مختلف اقسام: ریاضی میں ، ریاضی میں مختلف نوعیت کا تعلق ہرمیئن سمتار جگہ کی ہے جو وابستہ الجبرک جھوٹے گروپ کے ریاضی کے ایک گروہوں کے ذریعہ ہوتا ہے۔
ریاضی کی zeta_function / ریاضی کے زیٹا فنکشن: ریاضی میں ، ریاضی کا جیٹا فنکشن ایک جیٹا فنکشن ہوتا ہے جس سے منسلک ہوتا ہے جو اعداد انفرادی حد سے زیادہ کی قسم کی ہے۔ ریاضی جیٹا فنکشن ریمن زیٹا فنکشن اور ڈیڈکائنڈ زیٹا فنکشن کو اعلی طول و عرض میں جدا کرتا ہے۔ حسابی زیٹا فنکشن نظریہ نمبر کی سب سے بنیادی چیزوں میں سے ایک ہے۔
ارڈی میٹیکا / ارڈی میٹیکا: ریاضی کا ایک قدیم یونانی متن ہے جسے ریاضی دان ڈیوفانٹس نے تیسری صدی عیسوی میں لکھا تھا۔ یہ 130 الجبرای پریشانیوں کا ایک مجموعہ ہے جس میں طے شدہ مساوات اور غیر یقینی مساوات کا عددی حل ملتا ہے۔
اریڈی میٹیکا انفینیٹورم / جان والیس: جان والس ایک انگریز پادری اور ریاضی دان تھا جنہیں لاتعداد کیلکولوز کی نشوونما کا جزوی اعتبار دیا جاتا ہے۔ 1643 اور 1689 کے درمیان انہوں نے پارلیمنٹ اور بعد میں شاہی عدالت کے چیف کرپٹوگرافر کی حیثیت سے خدمات انجام دیں۔ اسے علامت od متعارف کرانے کا سہرا ہے جو لامحدودیت کے تصور کی نمائندگی کرتا ہے۔ اس نے اسی طرح 1 / ∞ کا استعمال غیر منحصر کے لئے کیا۔ جان والیس نیوٹن کے ہم عصر اور ریاضی کی ابتدائی نشاna ثانیہ کے سب سے بڑے دانشور تھے۔
اریڈی میٹیکا لوگرتھمیکا / ہنری برگز (ریاضی دان): ہنری بریگز انگریزی کے ریاضی دان تھے جنہوں نے جان نیپیئر کے ذریعہ ایجاد کردہ اصل لاجارتھم کو عام لوگارتھم میں تبدیل کرنے کے لئے قابل ذکر تھا ، جو کبھی کبھی اس کے اعزاز میں برگیسیئن لوگارڈم کے نام سے جانے جاتے ہیں۔ جدید استعمال میں طویل تقسیم کے ل The مخصوص الگورتھم کو بریگزٹ سی نے متعارف کرایا تھا ۔ 1600 ء۔
Arithmetica Universalis / Arithmetica Universalis: ایریٹمیٹیکا یونیورالیس اسحاق نیوٹن کا ریاضی کا متن ہے۔ لاطینی میں لکھا گیا ، اس کی ترمیم اور کیمبرج یونیورسٹی میں ریاضی کے لوکاسین پروفیسر کی حیثیت سے ، نیوٹن کے جانشین ، ولیم ویسٹن نے شائع کی۔ اریتھمیٹیکا نیوٹن کے لیکچر نوٹ پر مبنی تھا۔
ریاضی کلاسیکی / دس کمپیوٹیشنل کینن: دس کمپیوٹیشنل کینن دس دس ریاضی کے کاموں کا ایک مجموعہ تھا جو ابتدائی تانگ خاندان کے ریاضی دان لی چونفینگ (602–670) نے ریاضی میں شاہی امتحانات کے سرکاری ریاضی کے متون کی حیثیت سے مرتب کیا تھا۔
ریاضی کی عبوری_ضروری / دوسرا حکم ریاضی: ریاضیاتی منطق میں ، دوسرا ترتیب ریاضی ریاضیاتی نظام کا ایک مجموعہ ہے جو قدرتی اعداد اور ان کے ذیلی منصوبوں کو باقاعدہ بناتا ہے۔ یہ ریاضی کے بہت سے ، لیکن سبھی کے لئے ایک بنیاد کے طور پر محوری سیٹ تھیوری کا متبادل ہے۔
حسابی الجبرا / جارج میور: جارج میور ایف آر ایس انگریز ریاضی دان اور انگلیائی عالم تھا۔ اس نے قائم کیا جسے منطق کا برطانوی الجبرا کہا جاتا ہے۔
حسابی الجبرا_جومیٹری / ریاضی ریاضی: ریاضی میں ، ریاضی ریاضی تقریبا rough الیگابرک جیومیٹری سے لے کر نمبر تھیوری میں دشواریوں تک کی تکنیک کا استعمال ہوتا ہے۔ ریاضی کا جیومیٹری ڈیوفانٹائن جیومیٹری کے ارد گرد مرکوز ہے ، الجبراic قسموں کے عقلی نکات کا مطالعہ۔
ریاضی اور_ لاجیکل_ یونیت / ریاضی کی منطق اکائی: کمپیوٹنگ میں ، ایک ریاضی کا منطق یونٹ (ALU) ایک مشترکہ ڈیجیٹل سرکٹ ہے جو عددی بائنری نمبروں پر ریاضی اور بٹویس آپریشن انجام دیتا ہے۔ یہ فلوٹنگ پوائنٹ یونٹ (FPU) کے برعکس ہے ، جو فلوٹنگ پوائنٹ نمبرز پر کام کرتا ہے۔ یہ کمپیوٹنگ سرکٹوں کی بہت سی اقسام کا بنیادی عمارت ہے ، جس میں کمپیوٹروں کی سنٹرل پروسیسنگ یونٹ (سی پی یو) ، ایف پی یو ، اور گرافکس پروسیسنگ یونٹ (جی پی یو) شامل ہیں۔
ریاضی کی افہام و تفہیم / دوسرا ترتیب ریاضی: ریاضیاتی منطق میں ، دوسرا ترتیب ریاضی ریاضیاتی نظام کا ایک مجموعہ ہے جو قدرتی اعداد اور ان کے ذیلی منصوبوں کو باقاعدہ بناتا ہے۔ یہ ریاضی کے بہت سے ، لیکن سبھی کے لئے ایک بنیاد کے طور پر محوری سیٹ تھیوری کا متبادل ہے۔
ریاضی کی افہام و تفہیم_کسیوم / دوسرا حکم ریاضی: ریاضیاتی منطق میں ، دوسرا ترتیب ریاضی ریاضیاتی نظام کا ایک مجموعہ ہے جو قدرتی اعداد اور ان کے ذیلی منصوبوں کو باقاعدہ بناتا ہے۔ یہ ریاضی کے بہت سے ، لیکن سبھی کے لئے ایک بنیاد کے طور پر محوری سیٹ تھیوری کا متبادل ہے۔
ریاضی کی تشکیل / تجریدی نمبر تھیوری: خلاصہ تجزیاتی نمبر تھیوری ریاضی کی ایک شاخ ہے جو کلاسیکی تجزیاتی نمبر تھیوری کے نظریات اور تراکیب لیتا ہے اور مختلف ریاضی کے مختلف شعبوں پر ان کا اطلاق کرتا ہے۔ کلاسیکی پرائم نمبر کا نظریہ ایک پروٹو ٹائپیکل مثال کے طور پر کام کرتا ہے ، اور اسماٹومیٹک تقسیم کے نتائج کو خلاصہ کرنے پر زور دیا جاتا ہے۔ یہ نظریہ بیسویں صدی میں جان نوپفماچر اور آرن بیرلنگ جیسے ریاضی دانوں نے ایجاد اور تیار کیا تھا۔
ریاضی کی تقریب / ریاضی کی تقریب: نمبر تھیوری میں ، ایک ریاضی ، ریاضی یا نمبر نظریاتی فعل زیادہ تر مصنفین کے لئے ہوتا ہے کوئی بھی فنکشن f ( n ) جس کا ڈومین مثبت عدد ہوتا ہے اور جس کی حد پیچیدہ اعداد کا سب سیٹ ہوتی ہے۔ ہارڈی اینڈ رائٹ ان کی تعریف میں یہ تقاضا بھی شامل کرتے ہیں کہ ایک ریاضی کی تقریب " n کی کچھ ریاضی کی خاصیت کا اظہار کرتی ہے"۔
ریاضی کے افعال / ریاضی کی تقریب: نمبر تھیوری میں ، ایک ریاضی ، ریاضی یا نمبر نظریاتی فعل زیادہ تر مصنفین کے لئے ہوتا ہے کوئی بھی فنکشن f ( n ) جس کا ڈومین مثبت عدد ہوتا ہے اور جس کی حد پیچیدہ اعداد کا سب سیٹ ہوتی ہے۔ ہارڈی اینڈ رائٹ ان کی تعریف میں یہ تقاضا بھی شامل کرتے ہیں کہ ایک ریاضی کی تقریب " n کی کچھ ریاضی کی خاصیت کا اظہار کرتی ہے"۔
ریاضی کی درجہ بندی / ریاضی کا درجہ بندی: ریاضیاتی منطق میں ، ریاضی کی درجہ بندی ، ریاضی کے تنظیمی ڈھانچے یا کلین – موسٹوسکی درجہ بندی کچھ فارموں کی درجہ بندی کرتی ہے جو ان کی وضاحت کرنے والے فارمولوں کی پیچیدگی پر مبنی ہوتی ہے۔ کوئی بھی سیٹ جو درجہ بندی حاصل کرتا ہے اسے ریاضی کہا جاتا ہے ۔
ریاضی کا مطلب / ریاضی کا مطلب: ریاضی اور اعدادوشمار میں ، ریاضی کا مطلب ، یا محض اسباب یا اوسط ، مجموعوں میں اعداد کی گنتی کے حساب سے تقسیم کردہ اعداد کے مجموعے کا مجموعہ ہے۔ یہ مجموعہ اکثر کسی تجربے یا مشاہداتی مطالعے کے نتائج کا ایک سیٹ ہوتا ہے ، یا اکثر کسی سروے کے نتائج کا ایک سیٹ ہوتا ہے۔ ریاضی اور اعدادوشمار کے کچھ سیاق و سباق میں "ریاضی کا مطلب" کی اصطلاح کو ترجیح دی جاتی ہے ، کیوں کہ اس سے اس کو دوسرے ذرائع سے ممتاز کرنے میں مدد ملتی ہے ، جیسے ہندسی مطلب اور ہارمونک وسیلہ۔
حسابی نمبر / ریاضی کا مجموعہ: ریاضیاتی منطق میں ، ریاضی کا ایک مجموعہ قدرتی اعداد کا ایک مجموعہ ہوتا ہے جس کی وضاحت پہلے آرڈر پیانو ریاضی کے فارمولے سے کی جا سکتی ہے۔ ریاضی کے سیٹ کو حسابی درجہ بندی کے ذریعہ درجہ بندی کیا جاتا ہے۔
ریاضی کی تعداد / ریاضی کے سیٹ: ریاضیاتی منطق میں ، ریاضی کا ایک مجموعہ قدرتی اعداد کا ایک مجموعہ ہوتا ہے جس کی وضاحت پہلے آرڈر پیانو ریاضی کے فارمولے سے کی جا سکتی ہے۔ ریاضی کے سیٹ کو حسابی درجہ بندی کے ذریعہ درجہ بندی کیا جاتا ہے۔
ریاضی کے عمل / ریاضی: ریاضی کی ریاضی کی ایک شاخ ہے جو اعداد کے مطالعہ پر مشتمل ہے ، خاص طور پر ان پر روایتی کارروائیوں کی خصوصیات کے علاوہ — اس کے علاوہ ، گھٹائو ، ضرب ، تقسیم ، کفارہ اور جڑوں کی کھوج۔ ریاضی شماری نمبر تھیوری کا ایک ابتدائی حصہ ہے ، اور عدد نظریہ کو الجبرا ، جیومیٹری اور تجزیہ کے ساتھ جدید ریاضی کی اعلی سطحی تقسیم میں سے ایک سمجھا جاتا ہے۔ ریاضی اور اعلی ریاضی کی اصطلاحیں 20 ویں صدی کے آغاز تک نمبر نظریہ کے مترادفات کے طور پر استعمال ہوتی تھیں اور بعض اوقات اب بھی عدد نظریہ کے وسیع حصے کا حوالہ دیتے ہیں۔
ریاضی کے عمل / ریاضی: ریاضی کی ریاضی کی ایک شاخ ہے جو اعداد کے مطالعہ پر مشتمل ہے ، خاص طور پر ان پر روایتی کارروائیوں کی خصوصیات کے علاوہ — اس کے علاوہ ، گھٹائو ، ضرب ، تقسیم ، کفارہ اور جڑوں کی کھوج۔ ریاضی شماری نمبر تھیوری کا ایک ابتدائی حصہ ہے ، اور عدد نظریہ کو الجبرا ، جیومیٹری اور تجزیہ کے ساتھ جدید ریاضی کی اعلی سطحی تقسیم میں سے ایک سمجھا جاتا ہے۔ ریاضی اور اعلی ریاضی کی اصطلاحیں 20 ویں صدی کے آغاز تک نمبر نظریہ کے مترادفات کے طور پر استعمال ہوتی تھیں اور بعض اوقات اب بھی عدد نظریہ کے وسیع حصے کا حوالہ دیتے ہیں۔
ریاضی کی ترقی / ریاضی کی ترقی: ایک ریاضی کی ترقی یا ریاضی کی ترتیب نمبروں کا ایک ایسا تسلسل ہے کہ لگاتار شرائط کے مابین فرق مستقل رہتا ہے۔ مثال کے طور پر ، تسلسل 5 ، 7 ، 9 ، 11 ، 13 ، 15 ،۔ .. ایک ریاضی کی ترقی ہے جو 2 کے عام فرق کے ساتھ ہے۔
ریاضی کا تناسب / اونٹیلٹی اور بلندی: خودمختاری اور یکسانیت وہ اصطلاحات ہیں جو ہیری پارچ کے ذریعہ متعارف کرائی گئی ہیں جن کی رنگت کی کلاسیں بالترتیب کسی مقررہ لہجے (شناخت) کے ہارمونکس یا سبحارونک ہیں۔ مثال کے طور پر: 1/1، 2/1، 3/1، ... یا 1/1، 1/2، 1/3، .... اوٹونالٹی وہ ہے جو عددی عوامل (... شناختوں ) کے ذریعہ تیار کردہ پچوں کا ایک مجموعہ ... حرف میں عددی مستقل سے زیادہ ہے۔ اس کے برعکس ، یوٹونالیٹی ایک اوٹونالٹی کی الٹ ہے ، عددی عوامل پر ... عددی عنصر میں اعداد میں مستقل عددی کے ساتھ گڑھوں کا مجموعہ ہے۔
ریاضی کی اصلی_نمبر / ریاضی کا سیٹ: ریاضیاتی منطق میں ، ریاضی کا ایک مجموعہ قدرتی اعداد کا ایک مجموعہ ہوتا ہے جس کی وضاحت پہلے آرڈر پیانو ریاضی کے فارمولے سے کی جا سکتی ہے۔ ریاضی کے سیٹ کو حسابی درجہ بندی کے ذریعہ درجہ بندی کیا جاتا ہے۔
ریاضی کی کمی / ریاضی کی درجہ بندی: ریاضیاتی منطق میں ، ریاضی کی درجہ بندی ، ریاضی کے تنظیمی ڈھانچے یا کلین – موسٹوسکی درجہ بندی کچھ فارموں کی درجہ بندی کرتی ہے جو ان کی وضاحت کرنے والے فارمولوں کی پیچیدگی پر مبنی ہوتی ہے۔ کوئی بھی سیٹ جو درجہ بندی حاصل کرتا ہے اسے ریاضی کہا جاتا ہے ۔
ریاضی کی انگوٹی / ریاضی کی انگوٹھی: الجبرا میں ، ایک بدلنے والی رنگ R کو ریاضی سمجھا جاتا ہے اگر مندرجہ ذیل مساوی شرائط میں سے کسی میں یہ موجود ہے: لوکلائزیشن R پر ہر ایک زیادہ سے زیادہ مثالی کے لئے ایک غیر عسکری رنگ ہے R کے تمام نظریات کے لئے ، اور ، تمام نظریات کے لئے ، اور ،